 |
| Nome - Tetraedro; Faces - 4; Arestas - 6; Vértices - 4; Vértices por face - 3; Encontros de faces em cada vértice: 3; Configurações de Vértices - 3.3.3; Grupo de Simetria - Td |
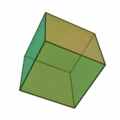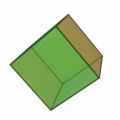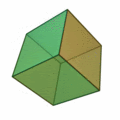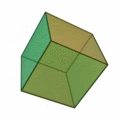 |
| Nome - Hexaedro (cubo); Faces - 6; Arestas - 12; Vértices - 8; Vértices por face - 4; Encontros de faces em cada vértice: 4; Configurações de Vértices - 4.4.4; Grupo de Simetria - Oh |
 |
| Nome - Octaedro; Faces - 8; Arestas - 12; Vértices - 6; Vértices por face - 3; Encontros de faces em cada vértice: 4; Configurações de Vértices - 3.3.3.3; Grupo de Simetria - Oh |
 |
| Nome - Dodecaedro; Faces - 12; Arestas - 30; Vértices - 20; Vértices por face - 5 Encontros de faces em cada vértice: 3; Configurações de Vértices - 5.5.5; Grupo de Simetria - Ih |
 |
| Nome - Icosaedro; Faces - 20; Arestas - 30; Vértices - 12; Vértices por face - 3 Encontros de faces em cada vértice: 5; Configurações de Vértices - 3.3.3.3.3; Grupo de Simetria - Ih |
Poliedros Duais:
 |
| Dual do Tetraedro é o Tetraedro. |
 |
| Dual do Cubo é o Octaedro e vice versa. |
 |
| Dual do Octaedro é o Cubo e vice versa. |
 |
| Dual do Dodecaedro é o Icosaedro e vice versa. |
 |
| Dual do Icosaedro é o Dodecaedro e vice versa. |
Nenhum comentário :
Postar um comentário