Hipercubo
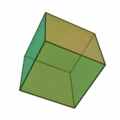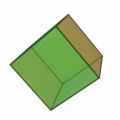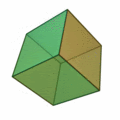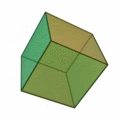
Em geometria, entende-se por hipercubo um análogo n-dimensional do quadrado (n=2) e do cubo (n=3). Todo hipercubo é fechado, compacto e convexo, cujo esqueleto é formado por grupos de segmentos paralelos alinhados em cada dimensão do espaço, formando ângulos retos com os outros segmentos de mesmo tamanho e comprimento.
Um n hipercubo-dimensional também é chamado de n-cubo. De acordo com o trabalho de HSM Coxeter (originalmente de Elte, 1912). A unidade de hipercubo é um hipercubo cujo lado tem uma unidade de comprimento. Muitas vezes, o hipercubo cujos cantos (ou vértices ) são os 2elevado a n pontos em R elevado a n com coordenadas iguais a 0 ou 1 é chamado de "a" unidade de hipercubo.
Tesserato
Um tesserato (ou tesseracto), octácoro regular ou hipercubo de quatro dimensões é um polícoro (polítopo de quatro dimensões) regular análogo ao cubo (que é um poliedro, um polítopo de três dimensões) e ao quadrado (que é um polígono, um polítopo de duas dimensões). Um octácoro apresenta vértices (pontos), arestas (linhas), faces (planos) e células (sólidos).
Como um quadrado é formado de linhas perpendiculares e um cubo é feito de quadrados perpendiculares, estende-se o raciocínio para a quarta dimensão: um tessarato é feito de cubos perpendiculares. Isso só se faz possível se houver uma quarta dimensão, simultaneamente perpendicular às três outras.
De acordo com o Oxford English Dictionary, o termo foi cunhado por Charles Howard Hilton, no livro A New Era of Thought.
História do Tesserato.
O tesserato é um análogo ao quadrado e ao cubo, mas com quatro dimensões. Para entendermos a quarta dimensão, é necessário relembrarmos rapidamente alguns conceitos de geometria. O primeiro conceito é o ponto. Um ponto é a representação geométrica de posição no espaço, e não possui dimensões (nem altura, nem comprimento, nem profundidade), ou seja, é impossível "medir" um ponto.
- Um ponto que se move em uma direção gera um segmento de reta.
- Uma linha que se desloca produz ou uma linha mais longa, ou uma área, se ela se move em direção perpendicular à sua direção anterior, ela gera um retângulo, e, se a distância for a mesma que a que o ponto se deslocou, um quadrado.
- Um quadrado, movendo-se nesta mesma distância em uma direção perpendicular, gera um cubo. Para mover o cubo, não podemos visualizar em que direção ele se moveria, assim como uma terceira dimensão seria invisível a habitantes presos à superfície de uma mesa, mas supondo-se que existisse uma direção perpendicular às três dimensões, e que o cubo se deslocasse nesta dimensão da mesma distância padrão, a figura gerada seria um tessarato.
- Para representarmos geometricamente um hipercubo de quarta dimensão, devemos nos socorrer outra vez da analogia: para formarmos um quadrado, unimos dois segmentos de reta paralelos e de mesmo comprimento através de seus extremos por outros dois outros segmentos de reta. Para representarmos um cubo, unimos os vértices de dois quadrados por quatro segmentos de reta. Para representarmos um hipercubo, unimos todos os vértices de dois cubos por segmentos de reta, conforme sugere a imagem.
in:
- wiki hipercubo
- wiki tesserato